Water Leaving A Spout

Posted byAlex BPosted inUncategorizedTags:

This is a problem I realized could be solved easily with a simplification of the Navier-Stokes equations. The problem asks, “What shape does water make when it exits a spout, such as from a kitchen sink?”

First begin by assuming the flow leaving the tank is not viscous, incompressible, not time varying, and the flow varies with the z and radial directions only. Use an axis-symmetric coordinate system with positive-z aligned with gravity. The key equations (continuity and momentum in the vertical and radial directions) are presented in their reduced form after applying the aforementioned assumptions:

\frac{1}{r} \frac{\partial r u_r}{\partial r} + \frac{\partial u_z}{\partial z} =0

\rho u_r \frac{\partial u_r}{\partial r} + u_z \frac{\partial u_r}{\partial z} = -\frac{\partial P}{\partial r}

\rho u_z \frac{\partial u_z}{\partial z} = \rho g z

The third equation can easily be solved recalling the identity,

u_z \frac{\partial u_z}{\partial z} = \frac{1}{2} \frac{\partial u_z^2}{\partial z}

from which one obtains (in addition to specifying the initial velocity at z = 0),

u_z(z) = \sqrt{2gz + u_{z0}^2}

At this point we may choose to solve for the velocity field. While this will be done, it is not necessary to ascertain to answer our original question. The radial velocity may be obtained using the continuity equation. First,

\frac{\partial u_z(z)}{\partial z} = \frac{g}{\sqrt{2gz + u_{z0}^2}}

Then, by a quick substitution and integration,

u_r = -\frac{gr}{2\sqrt{2gz + u_{z0}^2}}+ \frac{C}{r}

It can be shown that C = 0 by specifying the velocity at r = 0 is 0.

To obtain the actual shape of the water, one can apply the integral form of conservation of mass.

\rho_0 U_0 A_0 = \rho_1 U_1 A_1

Incompressibility assumes the density is invariant, further assume the spout shape is perfectly circular. By taking planar slices of the water leaving the faucet, only the z velocity is of our concern, then a formula for the radius can be created by using the beginning of the spout as a reference point. Note, the reference point used is not unique in that any point in the plane parallel to the spout exit may be specified.

u_{z0} \pi R_0^2 = u_z \pi R(z)^2

or

R(z) = \sqrt\frac{u_{z0} R_0^2}{u_z}

with simple substitution, the answer is obtained:

R(z) = \sqrt\frac{u_{z0} R_0^2}{\sqrt{2gz + u_{z0}^2}}

I am curious to see how accurate this formula describes reality. I bet this formula may have reasonable predictive power when (1) air is not entrained in the steam, (2) when the reference point is taken sufficiently far from the spout exit, and (3) when the stream diameter is wide enough to avoid dominant surface tension effects.

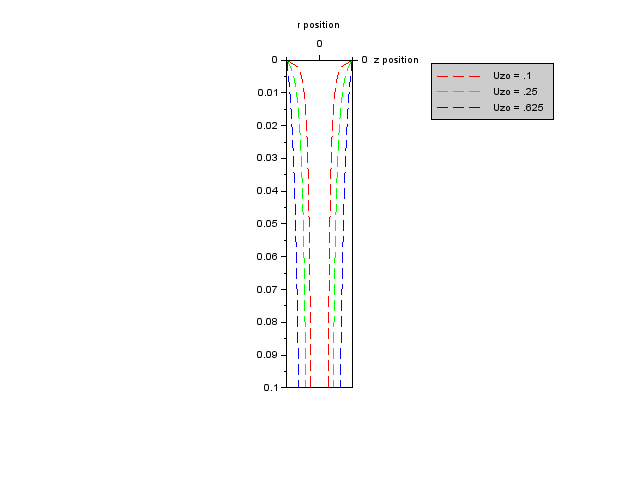
I have attached a figure below illustrating the result with Uzo = .1 to .625 m/s, r = .01 m, and z ranging from 0 to .1 m. This corresponds to a flow rate between roughly .5 to 3 gallons per minute. The figure was creating using Scilab.

Thank you for reading and I hope you found this short write up interesting.

Leave a comment